Measurements and Their Meanings
This chapter will explain how I, along with a colleague, measured Super Mario World and what conclusions I drew from those measurements. Everything that can be said about the smallest level of Super Mario World’s design comes down to one question: “How difficult is this jump?” Obviously, it’s a question that I asked thousands of times. Players don’t always consciously ask themselves this question, but it’s definitely in the back of their minds, especially on the really tricky jumps. Players have to predict the motion of Mario (or Luigi), the motion of their target, the distance they have to cross, any enemies they need to avoid while in flight, and numerous other factors that affect the difficulty of each individual action. Experienced players can do this in an instant, so it’s clear that these elements form a very cohesive whole. The problem for us as designers is figuring out how numerically hard a jump is. Can we unpack the intuitive understanding of this game that so many players have? Can we really break down Super Mario World into its constituent parts?
Fortunately, the answer is yes. In fact, Super Mario World breaks down quite nicely into its component design elements. From jumps, I was able to deduce challenges, and from challenges, I was able to realize the presence of cadences, and cadences fit together into skill themes. Going back to the beginning, my first task was to figure out ways to meaningfully measure everything in the game. Once everything was measured, things like cadences and skill themes came together quite quickly. This section tries to assemble the same line of thinking and process of discovery that I experienced while researching. The conclusions about these measurements are in the next chapter, but that chapter and the definitions in it will not make much sense without reading this one first.
Event Height, Event Width and D-Distance
The first and most important key to understanding the design of Super Mario World is the coin-block.

This block is the basic unit of measure in Super Mario World—the “atom” of the game. The hardware of the Super Nintendo required that images in the game conform to certain pixel sizes to optimize the file size of assets. Thus, there are no playable surfaces anywhere in the game that are not made up of an integer block length. There are no heights that are not made up of a whole number of blocks. Some moving platforms pass through heights that are not evenly divisible by blocks, but even these come to rest at block-level. Some objects appear to sit in spaces not evenly divisible by a coin-block, too, but their “hit box” is almost always at an effective integer mark. Therefore, every jump event in the game, even underwater events, can be measured precisely.
Mario’s ability to jump to any given height is dependent upon the amount of momentum he has. With no momentum, Mario can jump on top of a platform four blocks above the position of his feet. With one block of lateral momentum he can jump to a platform five blocks above the level of his feet. With eleven blocks of momentum, he can jump as high as the top of the sixth block above his feet.
If he has the cape, 11 blocks of momentum will enable Mario to soar high enough that measuring that height is pointless. You’ll notice, of course, that these momentum levels correspond to block-lengths. The 11-block momentum benchmark is important because it frequently prevents Mario from using the soaring cape ability to bypass levels (or sections of levels) that lack platforms of sufficient length. The designers of Super Mario World made level design easier on themselves by doing this; as long as they restricted platforms to lengths of less than 10, they could exert some control on how the player would approach a level.
There’s also the issue of how far Mario has to go laterally when jumping. Most jumps involve a lateral distance, which also breaks down nicely into block-lengths. At no momentum, Mario can jump from block one to block six, a distance of five blocks.
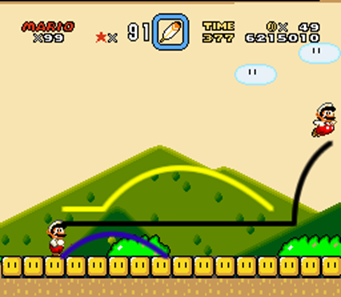
At any level of momentum before a full run, he can jump from block one to block nine (distance of eight), and at a full run he can cover 12 blocks. All of this, of course, assumes a flat area; any vertical distance involved in the jump will change the figures significantly. None of this takes into account the use of the cape powerup. The cape extends the fall time on a typical jump to about three times its normal length. It doesn’t significantly affect the speed of the lateral motion (what we’ll call the x vector), but by allowing the jump’s vertical motion (y vector) to last longer, jumps can go farther before Mario hits the ground again. Of course, the player can use the cape while at a full run to go so far across the level that measuring is pointless; only a wall, ceiling, or enemy will stop him.
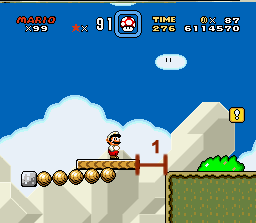
There are three important statistics that come out of these measurements: delta height, delta width, and d-distance. (Delta means the change between two or more points of data.) The most obvious place to start measuring jumps is the danger distance, or d-distance for short. This statistic is probably the most important one in this book. The d-distance is the amount of lateral distance that Mario has to cover in a single jump event. We don’t measure diagonally. Because of the way that vectors, intercepts and powerups in Super Mario World work, diagonals aren’t any more meaningful than the mere lateral distance unless there’s another element like an intercept present, and then it’s the intercept that’s really meaningful. D-distance measures the size of deadly obstacle Mario is trying to avoid, whether it’s a bottomless pit or some kind of damage floor (or, in some cases, a fall that forces the player to tediously climb back up).
The next most obvious point of study is changes in height during a jump event (delta height). In the jump pictured here, Mario is ascending. A number alone doesn’t explain if the jump is difficult, however, so let’s break it down further. This jump goes up; jumps that go up are more challenging than jumps that go down. The reason for this is that Mario loses his momentum when he’s going up (unless he’s flying with the cape or Blue Yoshi), but when going down his momentum tends to stay the same and can be easily controlled with a cape-glide. Anyone who has played the game will instantly know that the right hand jump pictured below is easier—even with a larger d-distance—because it is descending. When Mario begins a descending event, he usually has a lot more time to get into the right x-position. The y-position will take care of itself because of the pull of in-game gravity. Mario is already falling the whole time, so the player doesn’t really have to worry about that—especially if he has the cape, which will greatly extend the fall and give the player a ton of time to guide Mario downwards. There are exceptions to the rule, but it’s almost always harder to jump upwards than downwards.
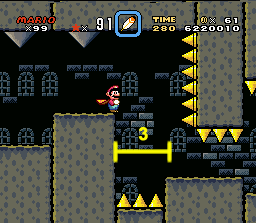
Want to read more? The rest of this section can be found in the print and eBook versions.